Choose control points for cubic bezier curves

Introduction

In common graphic environments (Java 2D, Postscript, wmf/emf/WinAPI, SVG) a cubic Bézier curve segment is drawn from two base- and two control points. I found lots of sourcecode for interpolating the pixels by given control points, but not how to choose them if i want to nicely interpolate a known function for a vector graphic.

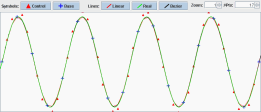
So i wrote a little playground in Java for cubic bezier curves as seen in

• java2d: PathIterator.SEG_CUBICTO / GeneralPath.curveTo
• postscript: curveto
• wmf/emf/Windows API/GDI: PolyBezier
• others ...

This is

• for choosing the right control points to send them to a graphics engine.
• for interpolate a known function.
• not for interpolating the pixels between the control points, the graphics engine will do this.
• quick and dirty, not optimized code, spit out to see what happens and to play with it.

Less theory

'Snip' from PathIterator.SEG_CUBICTO:

The Bézier curve is defined by a set of 3 points that specify a cubic parametric curve to be drawn from the most recently specified point. The curve is interpolated by the parametric control equation in the range (t=[0..1]) using the most recently specified (current) point (CP), the two control points (P1, P2) and the final point (P3):

P(t) = B(3,0)*CP + B(3,1)*P1 + B(3,2)*P2 + B(3,3)*P3 ; 0 <=t<=1 
mth coefficient of nth degree Bernstein polynomial:
	B(n,m) = C(n,m) * t^(m) * (1 - t)^(n-m) 
	C(n,m) = n! / (m! * (n-m)!)

which gives (Points: CP, P1, P2, P3)

	P(t) = (1-t)^3 * CP + 3(1-t)^2 t * P1 + 3(1-t)t^2 * P2 + t^3*P3
	P'(t) = [-3 (1 - t)^2] *CP + [3 - 12 t + 9 t^2] * P1 + [3 (2 - 3 t) t] * P2  [3 t^2] *P3
	P''(t) = [6(1-t)] * CP + [-6(2-3t)]*P1 + [6(1-3t)]*P2 + [6t]*P3

Maybe we can calculate the control points from the derivates of our known function.

	P'(t=0)  = P'  = -3*CP + 3*P1         
	P''(t=0) = P'' =  6*CP -12*P1 + 6*P2  
	               = -6*CP - 4*P' + 6*P2 
	=>
	P1= P'/3 +CP
	P2 = P''/6 +2P1 -CP= P''/6 +2/3P' +CP

An example bezier segment (rough sketch only):

                             P2
         P1
                .   .
          .             .
      .                    .
   .                         .
  .                           .
 .
CP                             .

                                P3

Some code

The slope of the interpolated curve at the base points should match the slope of our function, so we choose the control points on the tangent. I found it looks best if the distance of the control points to the base points is around 1/3. This is all i've done for now.

Get the application to play around with point distance. Choose other functions (sourcecode change needed).

Download application, sourcecode included: 16KB.
Start it with Java Webstart in a secure sandbox.
For the (simple) calculating parts look at BezierPanel#paintComponent().